陥没地帯 (195) - ノリの悪い日記

$2018$ 年度の神奈川県公立高校入試問題をやってみる. 正解率は $2.8 \%$ だそうである. 別解 $3$ はなかなか気づかなかった.

【問】

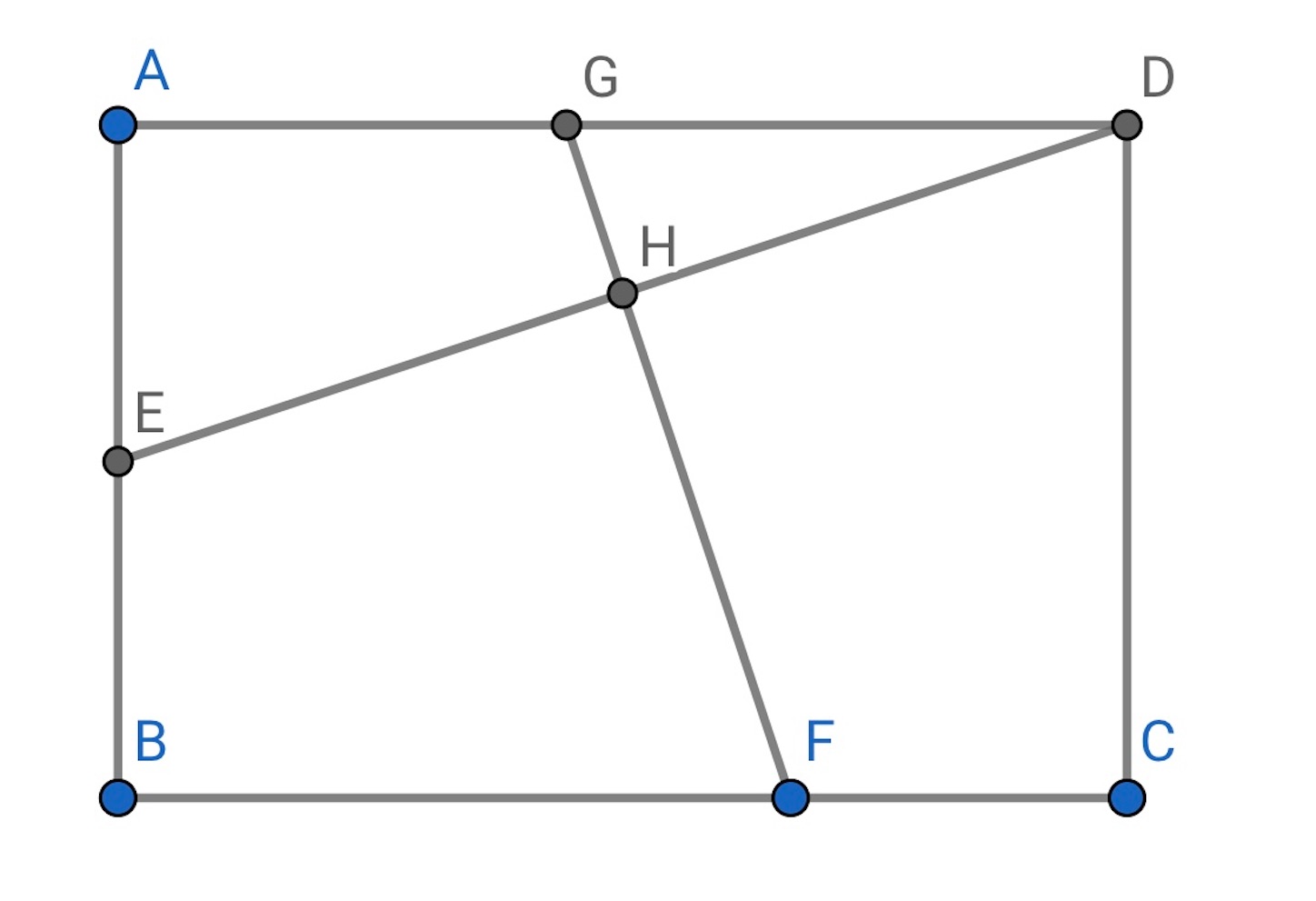
図のように長方形 $ABCD$ があり, 辺 $AB$ の中点を $E$ とする. また辺 $BC$ 上に点 $F$ を $BF: FC=2:1$ となるようにとり, 辺 $AD$ 上に $G$ を線分 $DE$ と線分 $FG$ が垂直に交わるようにとる. さらに線分 $DE$ と線分 $FG$ の交点を $H$ とする. $AB = 2 \mathrm{cm}$ , $BC = 3 \mathrm{cm}$ のとき, 線分 $GH$ の長さを求めなさい.

【解】

$G$ から $BC$ に垂線を下ろし, 垂線の足を $I$ とする. 四辺形 $EBFH$ は円に内接する. したがって, $\angle AED = \angle IFG$ であり, $\triangle DAE$ と $\triangle GIF$ は相似であることがいえる (円に内接することに気がつかなくてもこの相似は証明できる).

$IG : IF = AD:AE$ から $IF = 2/3$ であり, さらに $GD = 5/3$ であることもすぐにわかる. $\triangle DHG$ と $\triangle DAE$ は相似なので,

$GH: GD = EA: DE$ から,

$\displaystyle {GH: \frac{5}{3} = 1: \sqrt{10}}$

$\displaystyle{ GH = \frac{5}{3\sqrt{10}} = \frac{\sqrt{10}}{6} \ [cm]}$

である.//

※ 別解
$B$ を原点にとり, $\vec{BC}$ を $x$ 軸, $\vec{BA}$ を $y$ 軸とする. 直線 $ED$ の傾きは $1/3$ だから, 直交する直線 $GH$ の傾きは $-3$ である. $G(a, 2)$ とおくと,

$\displaystyle{\frac{-2}{2-a} = -3}$

したがって $a= 4/3$ である.
これから、 $GD = 5/3$ である. 後は同じ.//

※ 別解 $2$
$\triangle EBF \equiv \triangle FCD$ なので, $EF = FD$ から $\triangle FDE$ は二等辺三角形である. したがって $HE =HD$ である. $ED = \sqrt{10}$ であるから,

$\displaystyle{GH:\frac{\sqrt{10}}{2} = 1:3 }$

したがって,

$\displaystyle{GH = \frac{\sqrt{10}}{6}}$

である.//

※ 別解 $3$

上の図のように $A$ , $E$ , $F$ , $D$ が $H$ を中心とする半径 $\displaystyle{\frac{\sqrt{10}}{2}}$ の円周上にあることがわかる. $FG$ を延長して, その円周との交点を $J$ とする. $JEFD$ は一辺の長さが $\sqrt{5}$ の正方形である.