ノリの悪い日記

古今東西の映画、ポピュラー音楽、その他をいまここに交錯させながら随想します。

陥没地帯 (192)

初等幾何 高校数学

前の記事の続き. 過去の入試問題から.

【問】
(1) 三角形 ABC の内部の一点を M とするとき, MB + MC \lt AB + AC が成り立つことを証明せよ.
(2) 長方形 ABCD の辺 AD, CD 上にそれぞれ点 P, Q をとる. このとき, PB + PQ \leq AB + AQ が成り立つことを証明せよ.

【解】
(1) 前の記事で証明したので省略する.(誘導問題として残しておいた.)

(2)
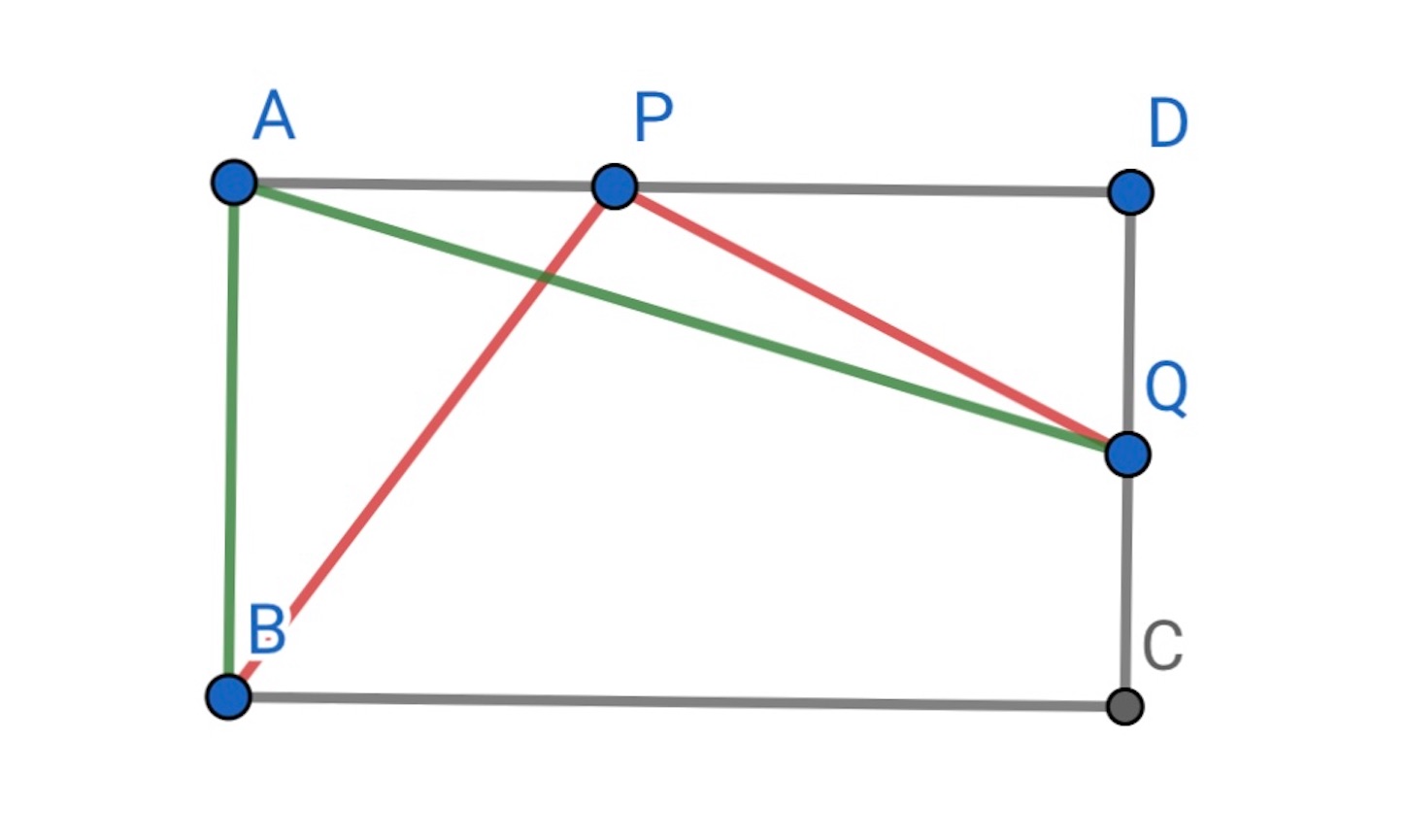
f:id:noriharu-katakura:20210606235538j:plain

図を描くと上のようになる. まず Q が D の位置にいるときは, 三角不等式を使って容易に,

PB + PQ \leq AB + AQ

が示せる (等号成立は, P が A の位置のとき) ので, 以降, Q は D の位置にはないとする.

すると, P が A の位置にあるときは, 等号が成立するのはすぐにわかる.

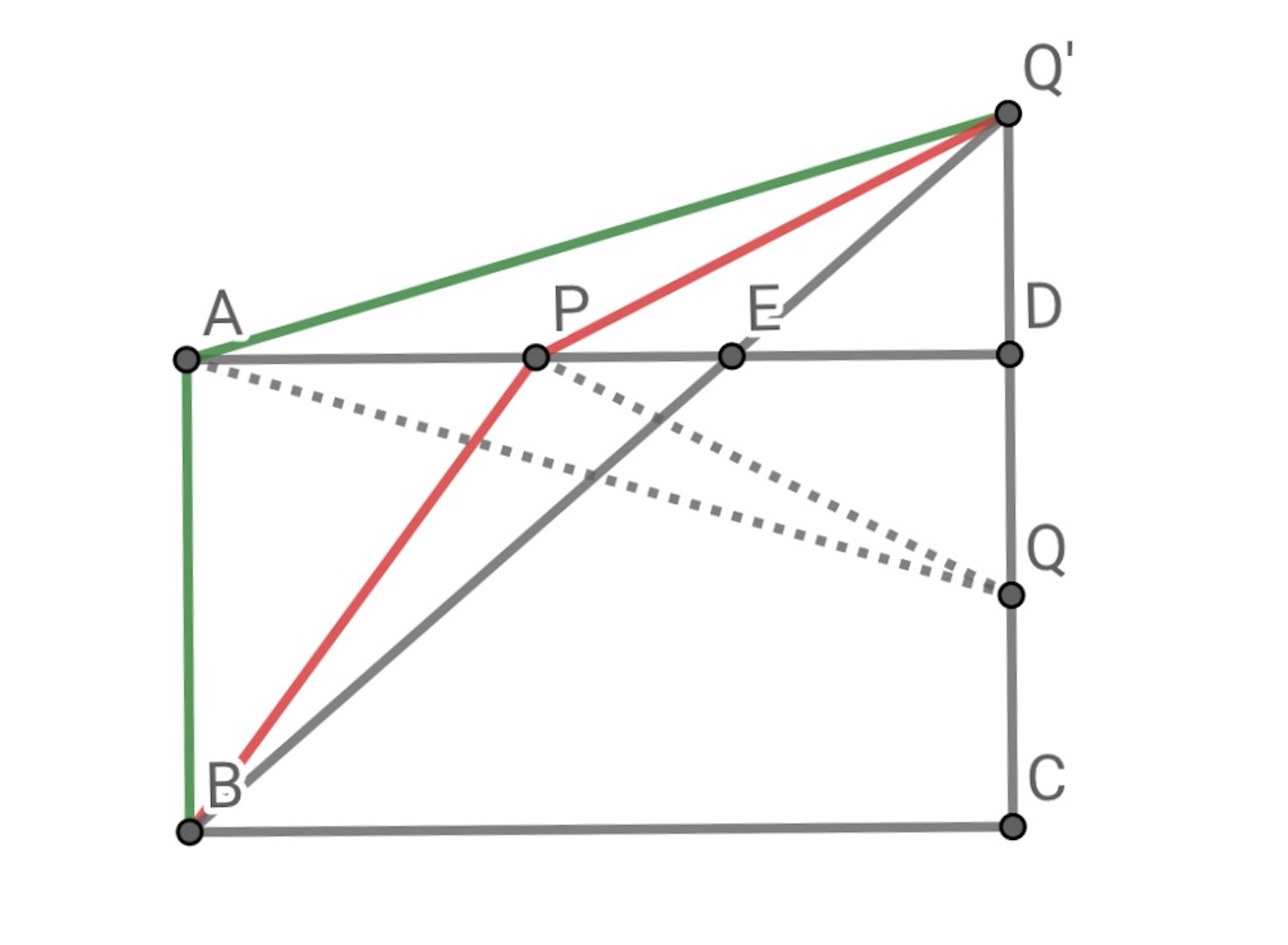
f:id:noriharu-katakura:20210606235819j:plain

CD を延長して Q' を DQ = DQ' となるようにとり, BQ' と AD の交点を E とする.

P が \triangle ABQ' の内部にある場合は, (1) の結果から,

PB + PQ' \lt AB + AQ'

である. PQ' = PQ, \ AQ' = AQ なので,

PB + PQ \lt AB + AQ

となる.

P が丁度 E の位置にいる場合は,

BQ'=PB + PQ' \lt AB + AQ'

から,

PB + PQ \lt AB + AQ

となる.

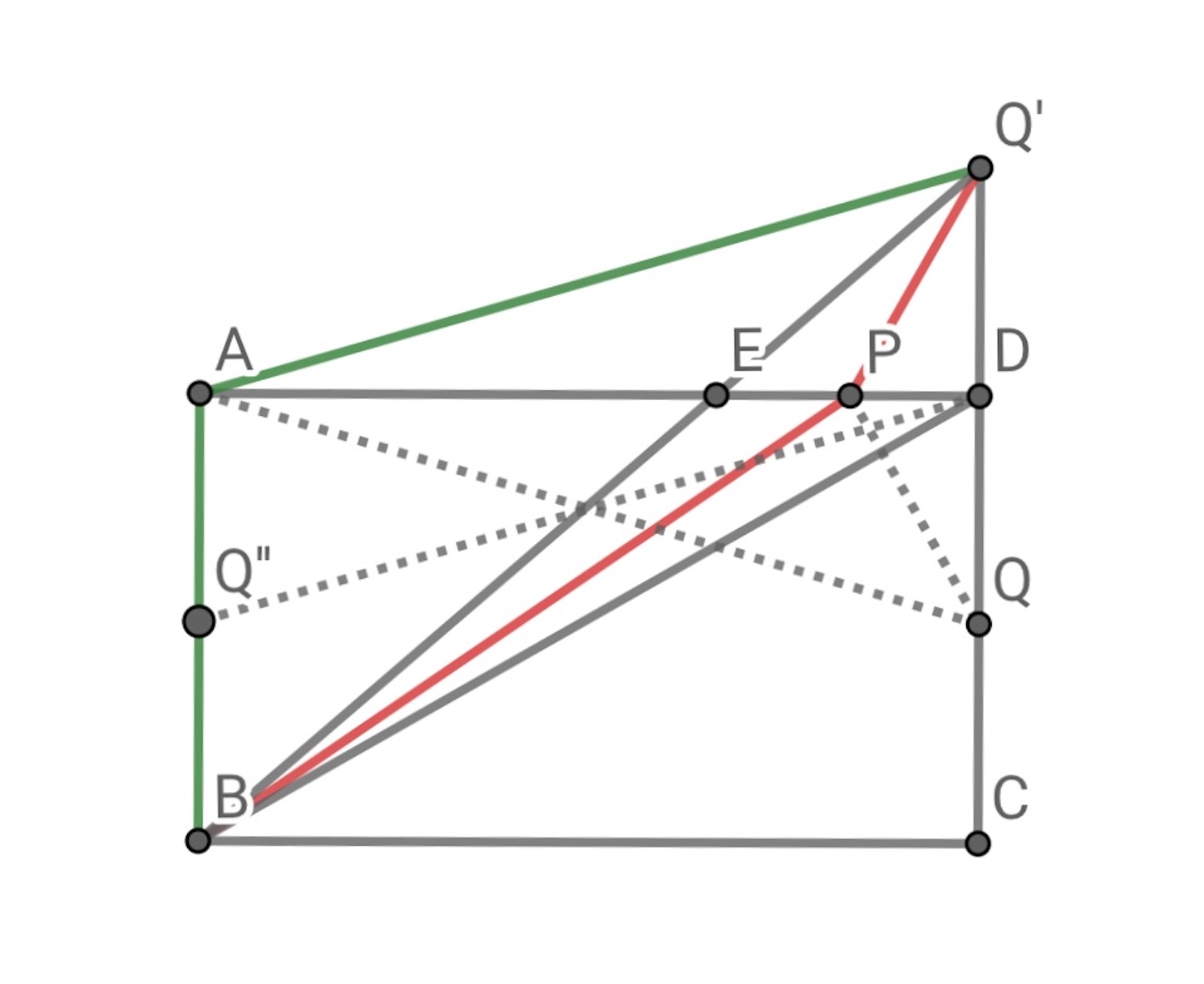
f:id:noriharu-katakura:20210607002559j:plain

P が \triangle BDQ' の内部にある場合は, 再び (1) の結果を使って,

PB+PQ' \lt DB + DQ'
PB+PQ \lt DB + DQ

となる.

AB 上に AQ" = DQ となるように Q" をとる. \triangle Q"BD を考えると,

Q"D = AQ
Q"B = AB - AQ" = AB -DQ

である. したがって,

DB \leq Q"D + Q"B = AB + AQ -DQ \\ DB + DQ \leq AB + AQ

となり (等号成立は Q が C の位置のとき),

PB + PQ \lt AB + AQ

である.

最後に P が D と一致する場合は,

PB + PQ = DB + DQ \leq AB + AQ

である (等号は Q が C の位置にあるとき).

以上, 題意は成立する.//