陥没地帯 (188) - ノリの悪い日記

円周角に関連して次の $2$ つの性質はよく知られている.

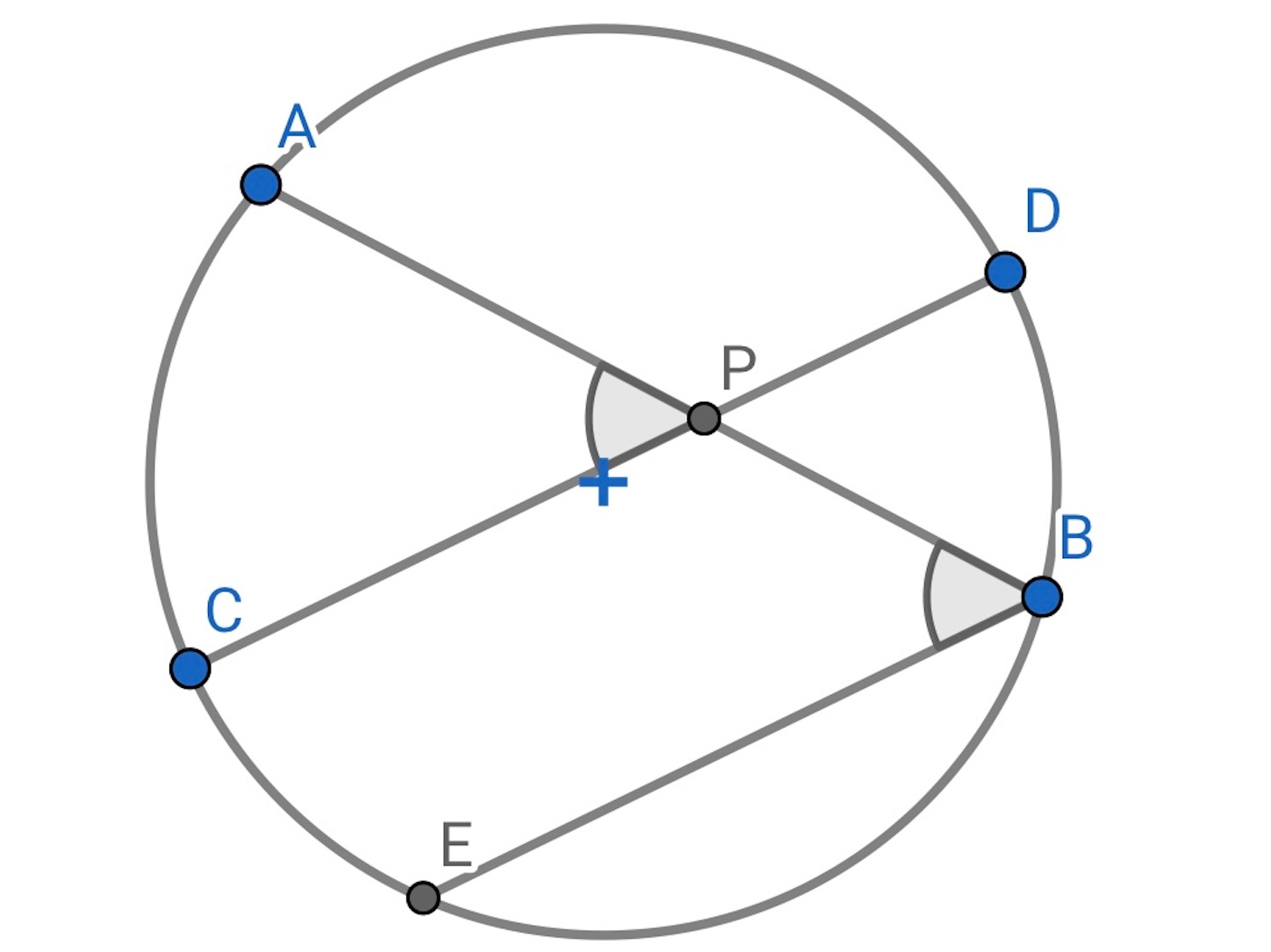
f:id:noriharu-katakura:20210601134750j:plain

i) 円の $2$ 弦 $AB$ と $CD$ が円の内部の点 $P$ において交わるときは, $\angle APC$ は, $\displaystyle {\stackrel {\huge \frown} {AC}+\stackrel{\huge\frown}{BD}}$ に等しい弧の上に立つ円周角に等しい.

【証明】
$\displaystyle {\stackrel {\huge \frown} {CE} = \stackrel {\huge \frown} {BD}}$ となるように, 円周上に点 $E$ をとれば, $CD \parallel EB$ である. したがって,

$\angle APC = \angle ABE$

となる.//

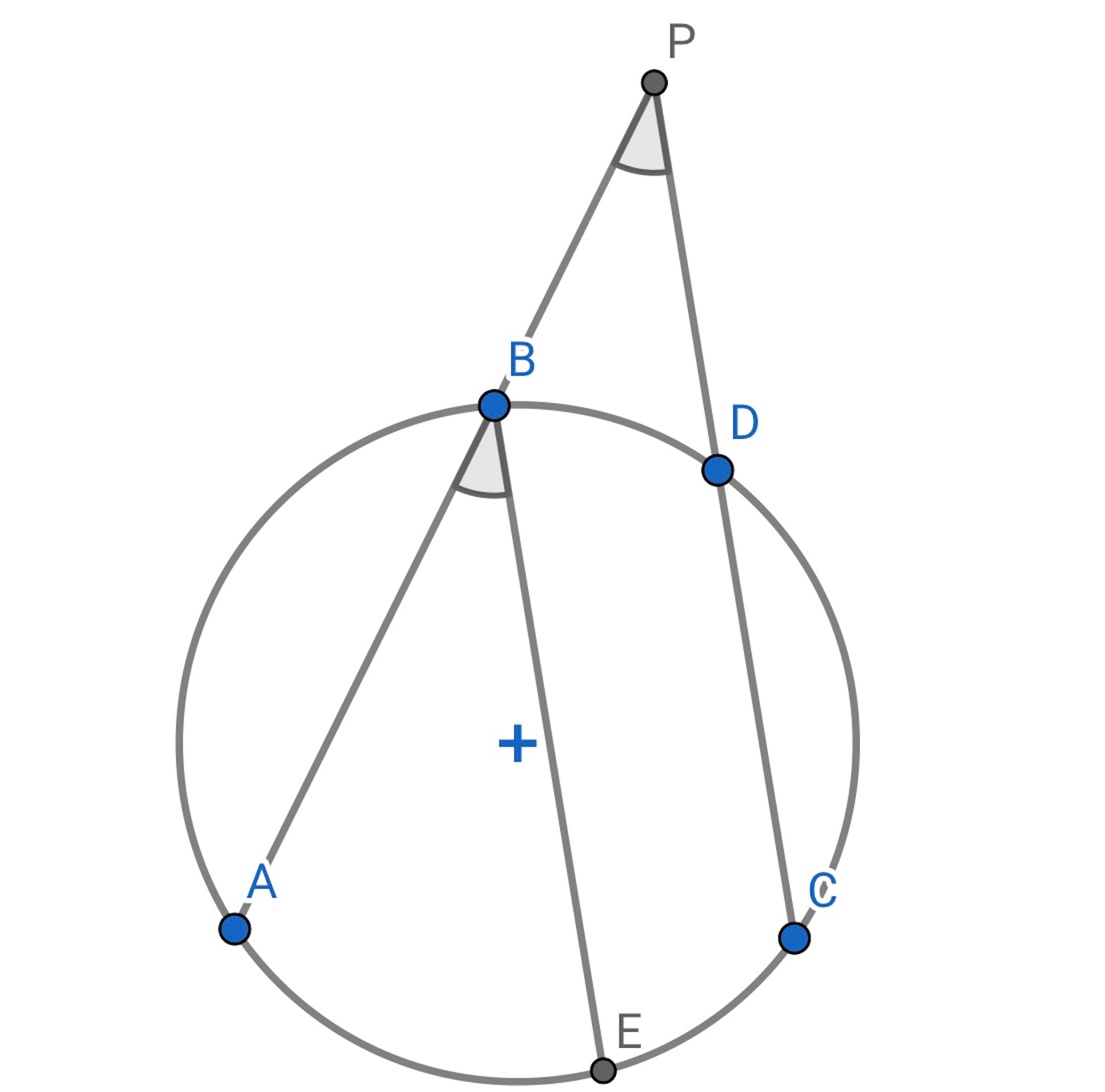
f:id:noriharu-katakura:20210601135658j:plain

ii) 円の $2$ 弦 $AB$ と $CD$ が円の外部の点 $P$ において交わるときは, $\angle APC$ は, $\displaystyle {\stackrel {\huge \frown} {AC}-\stackrel{\huge\frown}{BD}}$ に等しい弧の上に立つ円周角に等しい.

【証明】
i) と同様に証明できる.//

$\triangle ABC$ の外接円の弧 $\displaystyle {\stackrel {\huge \frown} {AB},\ \stackrel{\huge\frown}{AC}}$ の中点を $E$ , $F$ とする. $\angle A$ の二等分線 $AD$ と直線 $EF$ は直交する.

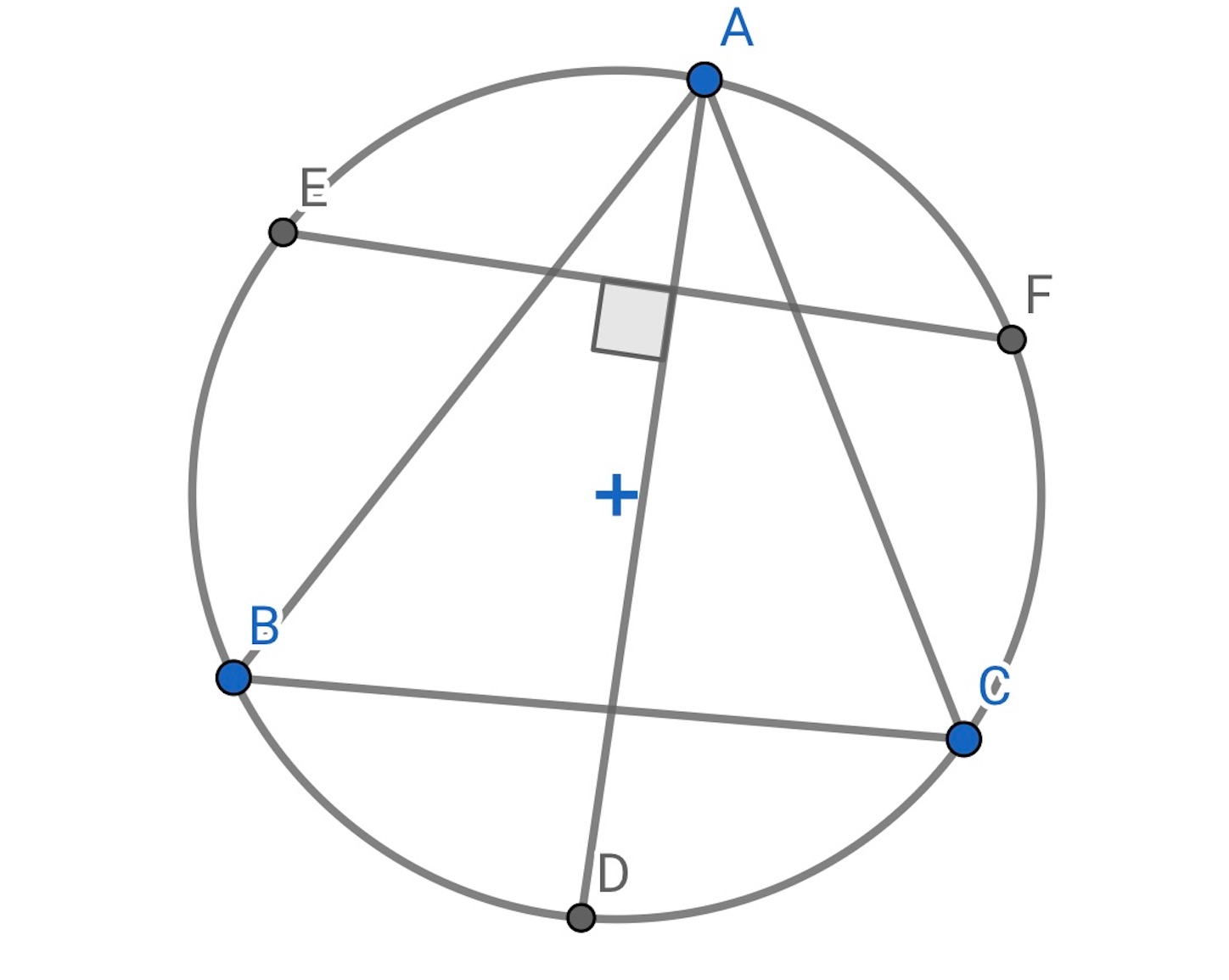
f:id:noriharu-katakura:20210601141648j:plain

弧 $\displaystyle {\stackrel {\huge \frown} {DE}+\ \stackrel{\huge\frown}{AF}}$ は円周の長さの半分である.//

三角形 $ABC$ の内心を $I$ とし, $AI$ の延長が外接円の周と交わる点を $D$ とすれば, $DB = DC = DI$ である.

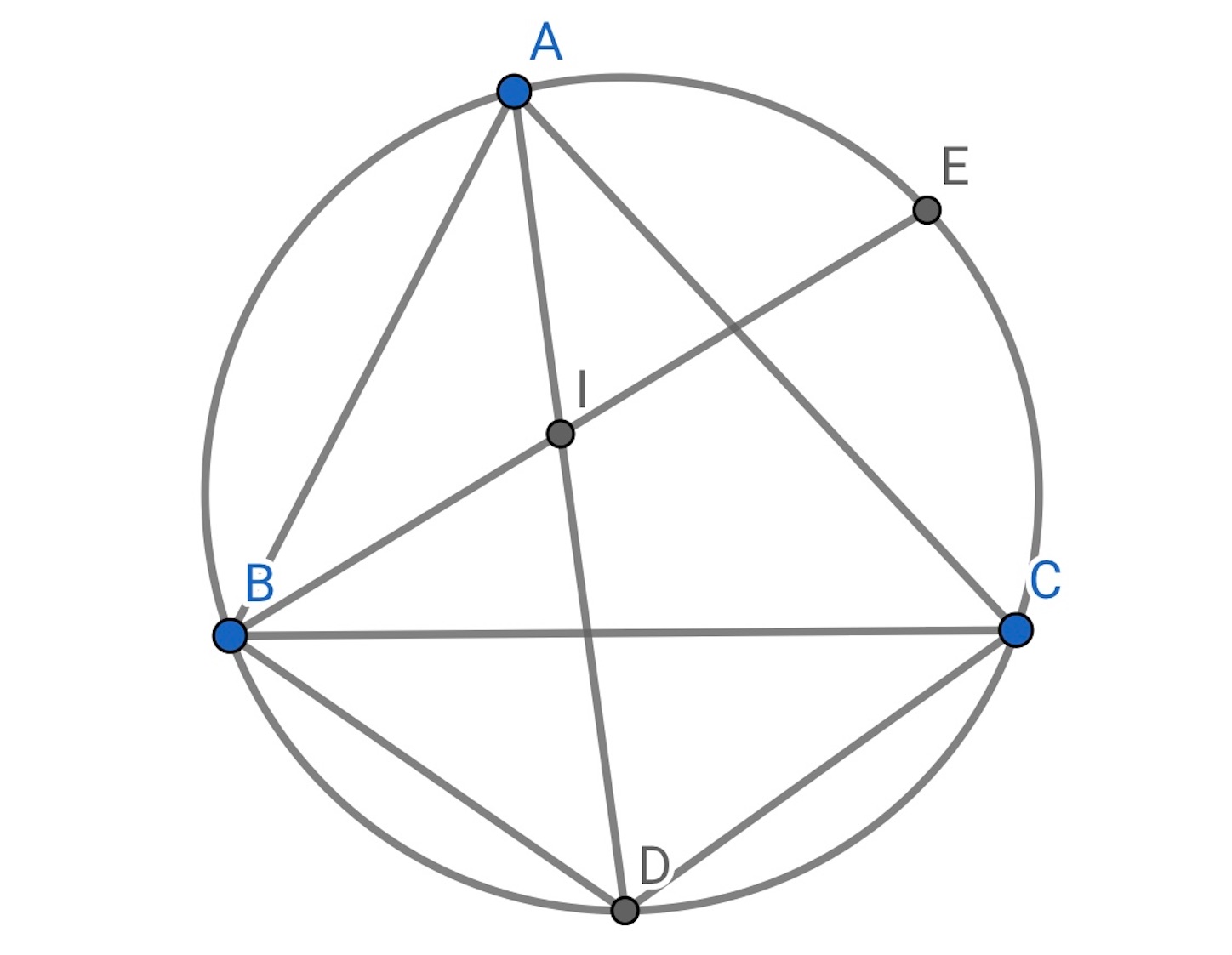
f:id:noriharu-katakura:20210601143408j:plain

$BI$ の延長が外接円の周と交わる点を $E$ とする.

$\displaystyle {\stackrel {\huge \frown} {AE}=\ \stackrel{\huge\frown}{CE}}$
$\displaystyle {\stackrel {\huge \frown} {BD}=\ \stackrel{\huge\frown}{CD}}$

だから,

$DB =DC$
$\angle BID = \angle DBE$

である. したがって,

$DB = DC = DI$

である.//

※ さらに, 傍心のひとつを $P$ とすれば, $\angle IBP = \angle ICP = 90^\circ$ から, $B$ , $I$ , $C$ , $P$ は同一円周上にあるので, $DB = DC = DI =DP$ であることがわかる.

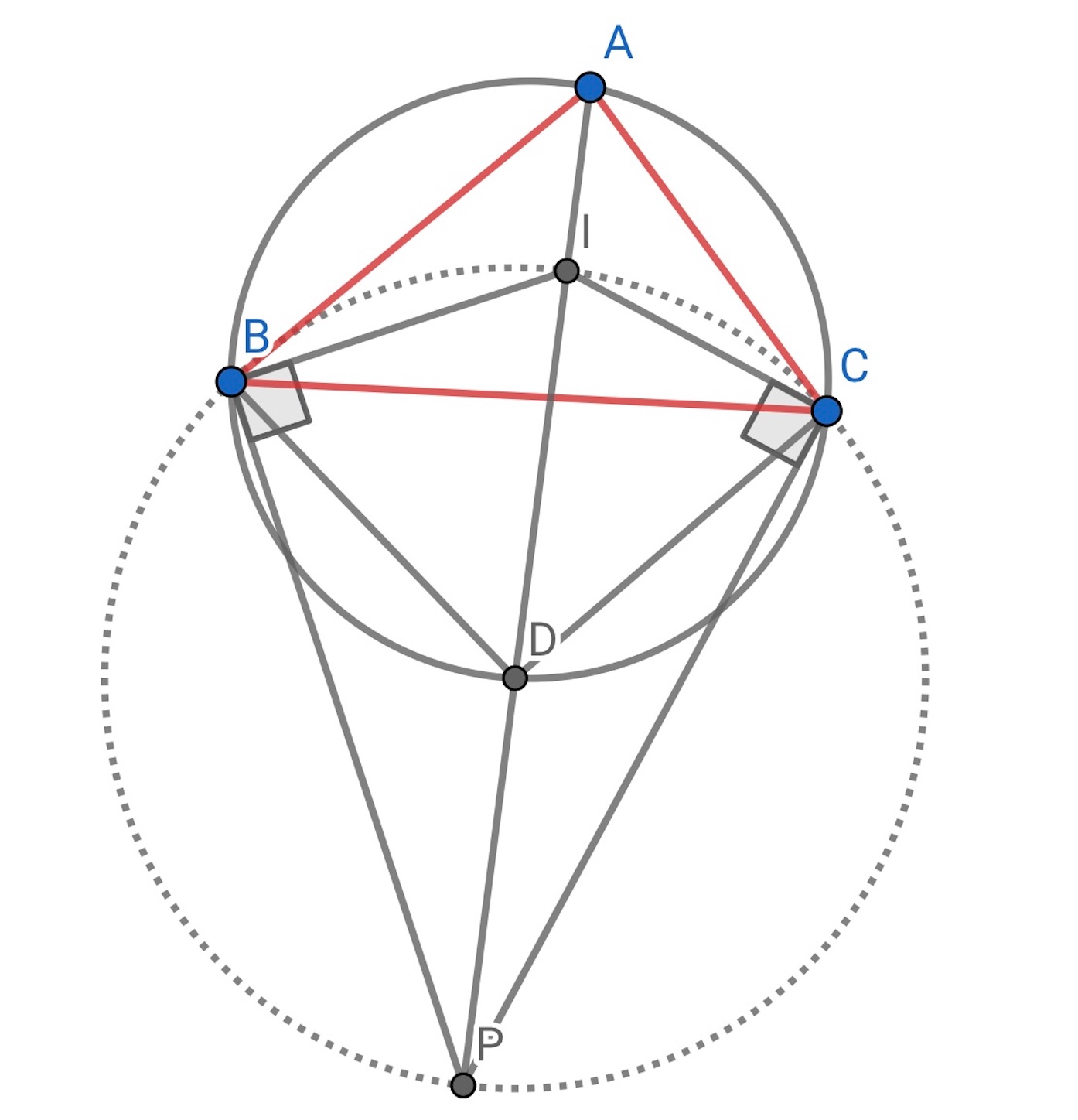
f:id:noriharu-katakura:20210602145208j:plain

実際, $\angle DBP = \angle DPB$ であることを示す.

$\displaystyle{\begin{align}\angle DBP &= \angle CBP - \angle CBD \\ &= \angle CIP - \angle CAD \\ &= \angle ACI \\ &= \angle BCI \\ &= \angle BPI \\ &= \angle DPB \end{align}}$

したがって, $D$ は, $B$ , $I$ , $C$ , $P$ を通る円の中心である.
//

※ 直前の結果を使って $N$ は傍心 $P$ , $Q$ を結ぶ線分の中点であることを示す.

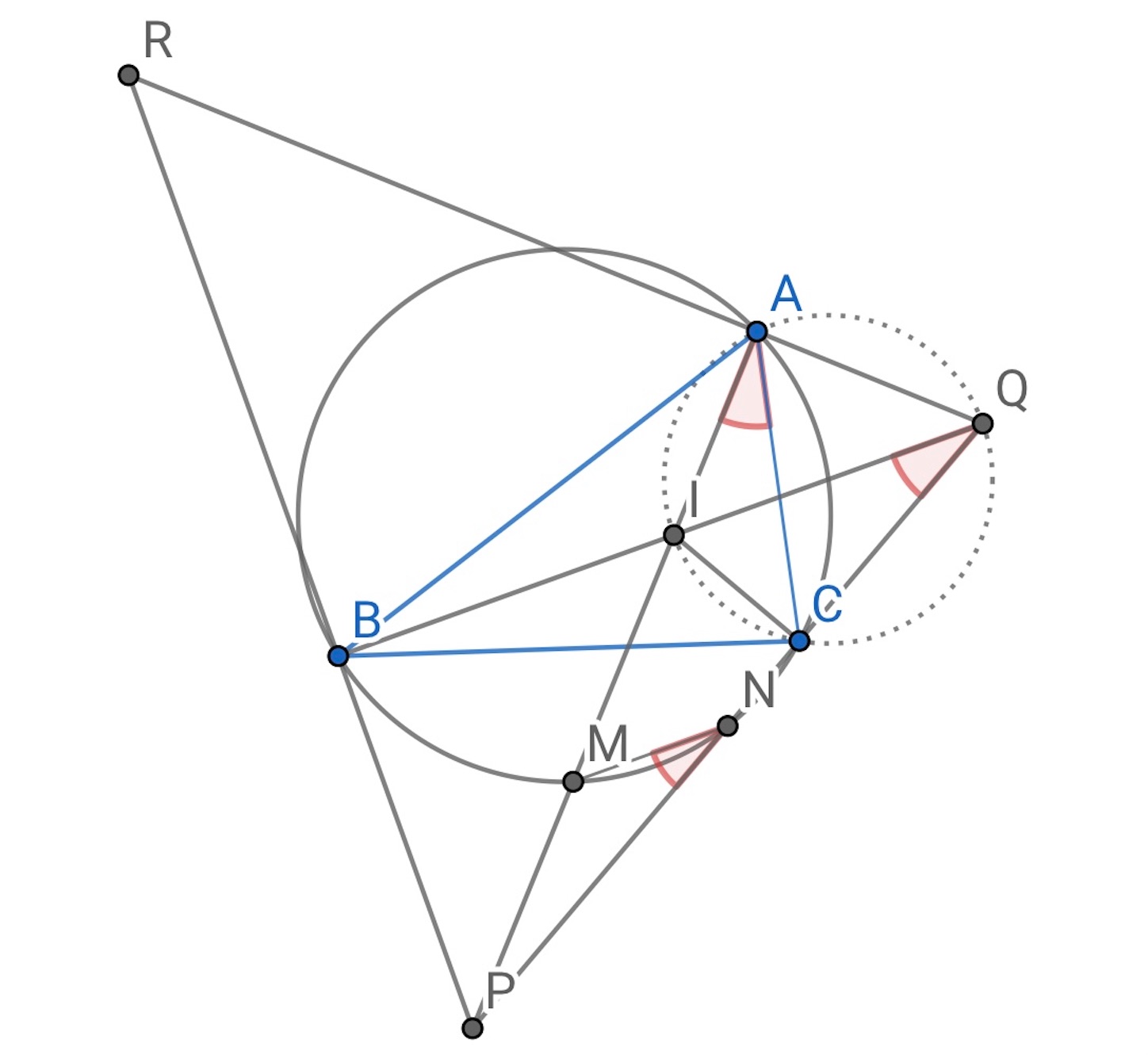
f:id:noriharu-katakura:20210604132353j:plain

$\triangle ABC$ の外接円に内接する四辺形 $AMNC$ を考えて,

$\angle MNP = \angle MAC$

四辺形 $AICQ$ は同一円周上にあるので,

$\angle MAC= \angle IQC$

したがって,

$\angle MNP = \angle IQC$

となり,

$MN \parallel IQ$

である. 直前の結果から $PM = MI$ なので, $N$ は、 $PQ$ の中点である.//

$\triangle ABC$ の内心を $I$ とする. また $\triangle ABC$ の外接円の半径を $R$ , 内接円の半径を $r$ とする. $AI$ の延長が, 外接円の周と交わる点を $D$ とすれば, $AI \cdot ID= 2Rr$ である.

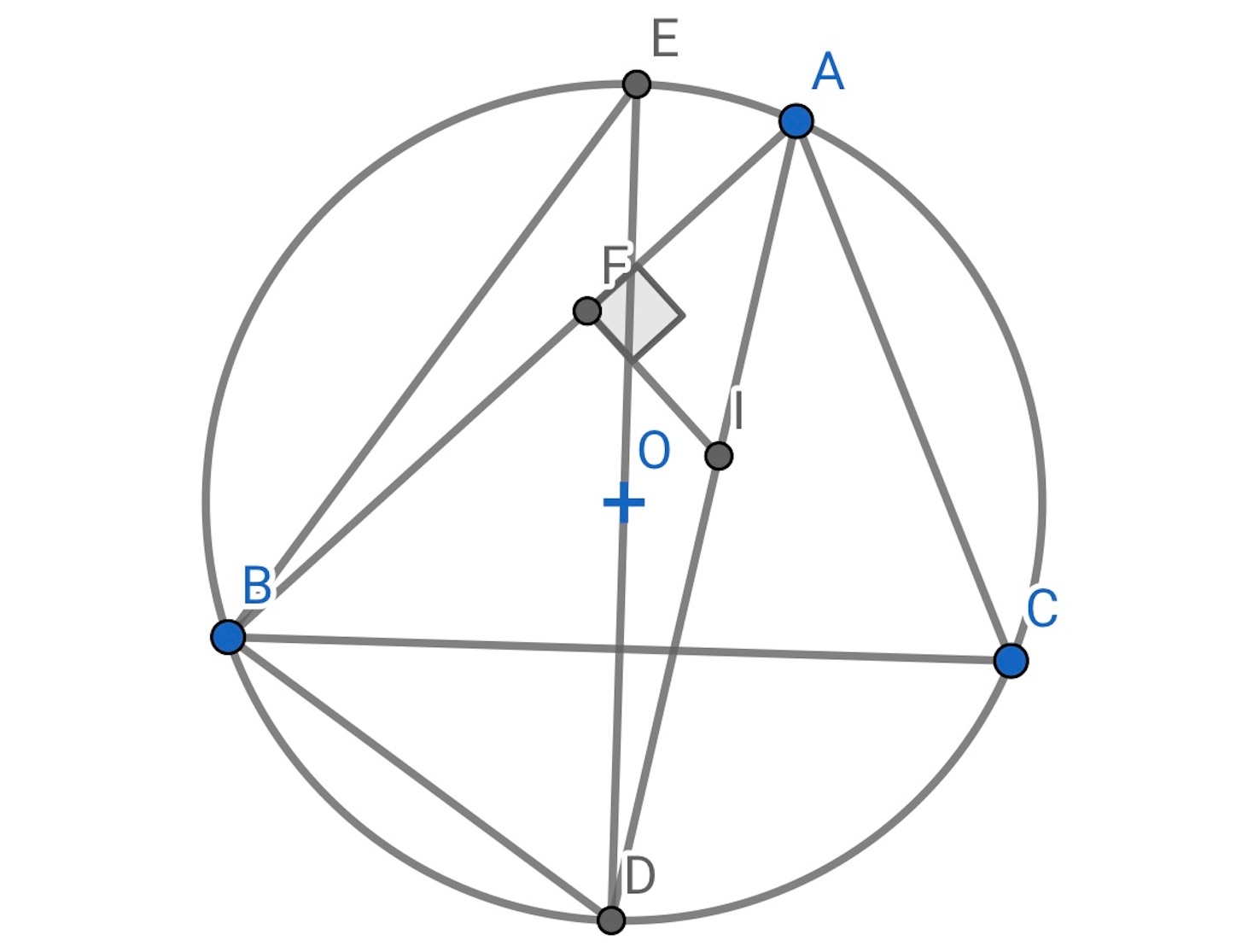
f:id:noriharu-katakura:20210601144438j:plain

$I$ から $AB$ に垂線を下ろし, その足を $F$ とすれば $IF = r$ である. $D$ から外接円の中心 $O$ を通る直線を引き, 外接円の円周と交わる点を $E$ とする. $DE = 2R$ である. $\triangle AFI$ と $\triangle EBD$ は相似だから,