ノリの悪い日記

古今東西の映画、ポピュラー音楽、その他をいまここに交錯させながら随想します。

ノリの悪い日記 https://www.port-k.com

陥没地帯 (181)

初等幾何

調和点列はいろいろなところに現れる.

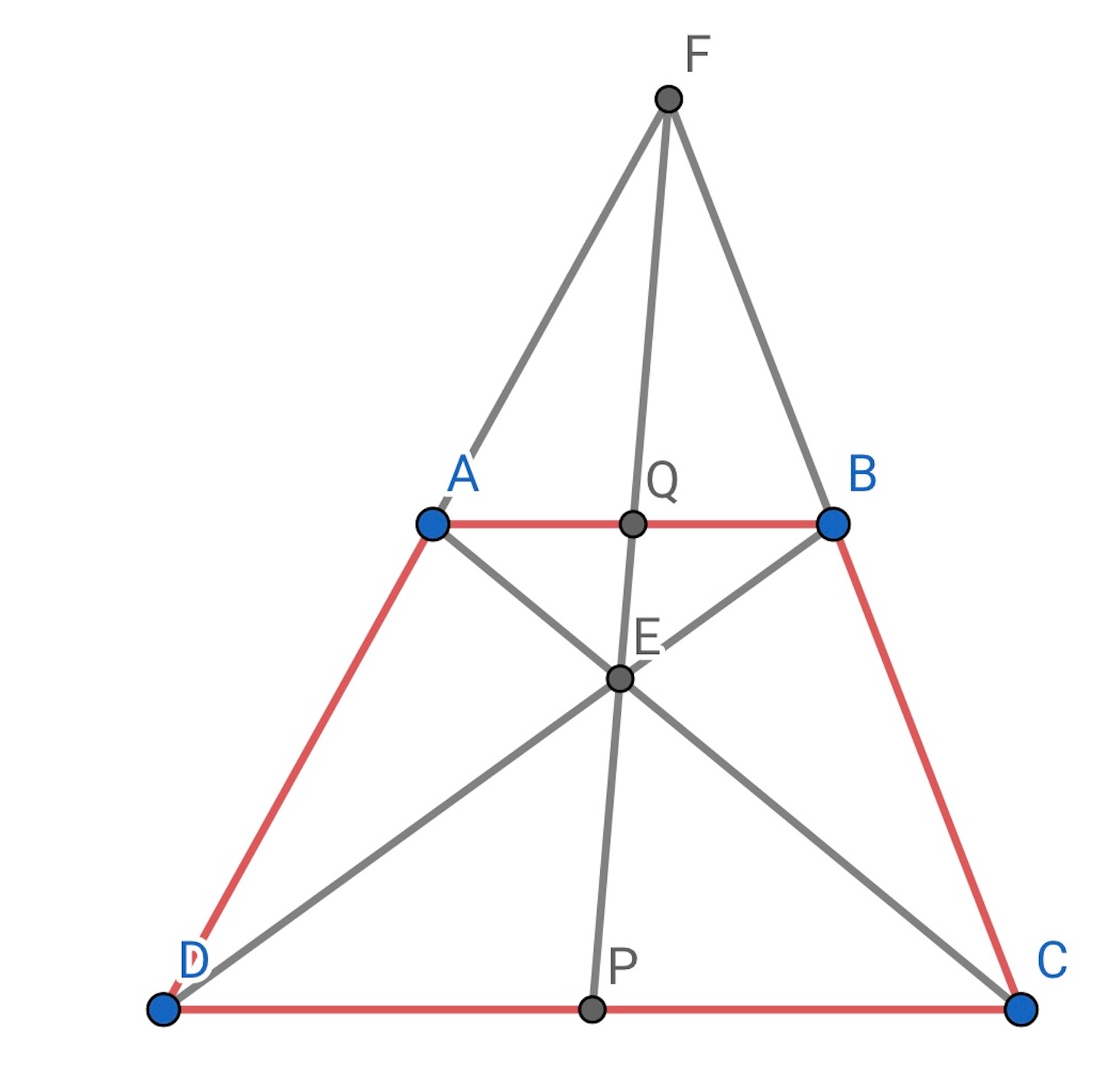
f:id:noriharu-katakura:20210519121150j:plain

台形 $ABCD$ の対角線の交点を $E$ とし, 辺 $DA$ と $CB$ の延長の交点を $F$ とする. $FE$ と $AB$ , $DC$ の交点をそれぞれ $P$ , $Q$ とする. そうすると, 点列 $P$ , $E$ , $Q$ , $F$ は調和点列である.

なぜなら, $\triangle FQB \sim \triangle FPC$ から,

$PF: FQ =FC:FB$

$\triangle FDC \sim \triangle FAB$ から,

$FC:FB=DC:AB$

$\triangle EDC \sim \triangle EBA$ から,

$DC:AB=EC:EA$

$\triangle ECP \sim \triangle EAQ$ から,

$EC:EA=PE:EQ$

故に,

$PF:FQ=PE:EQ$

したがって点列 $P$ , $E$ , $Q$ , $F$ は調和点列である.//

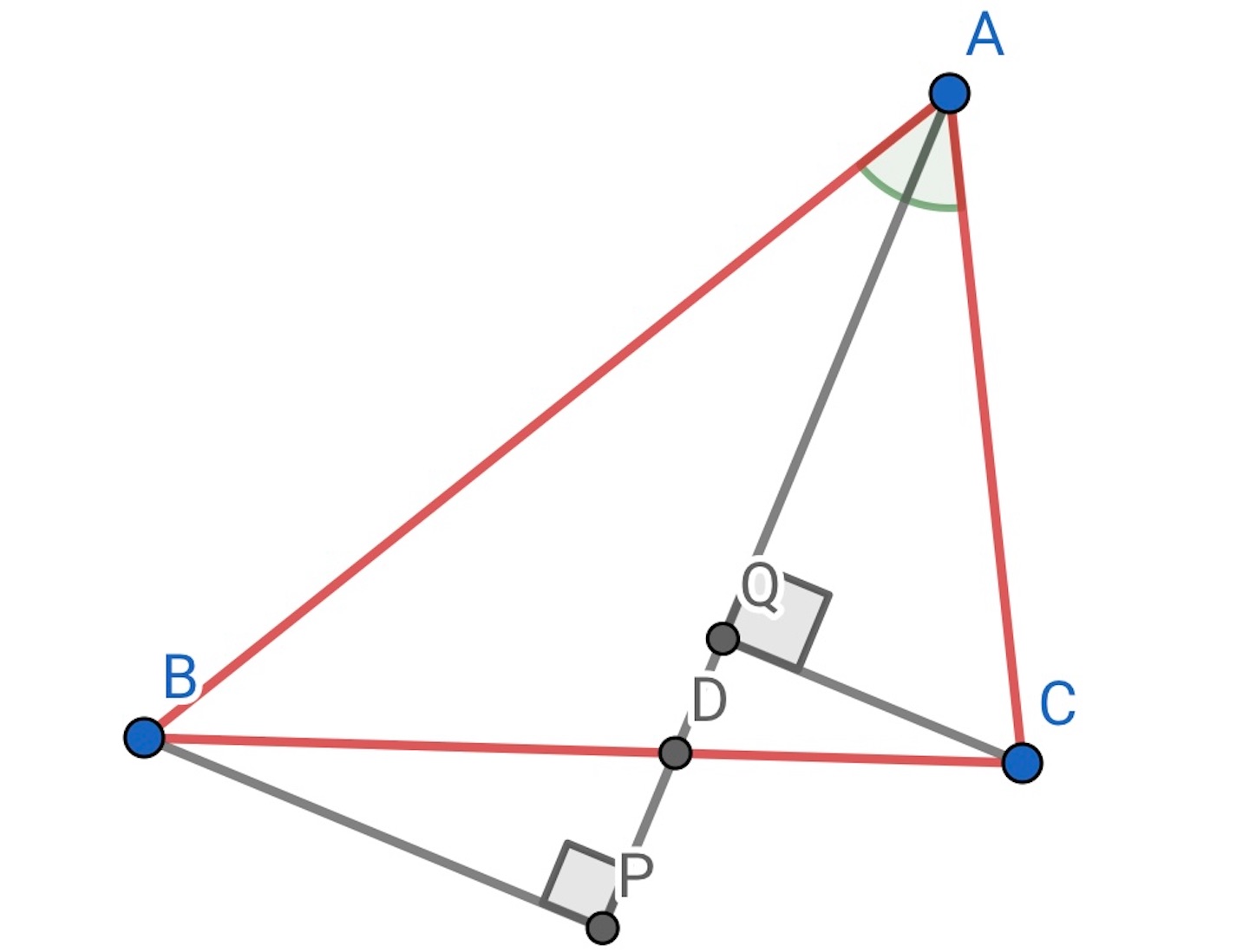
次の例. $\triangle ABC$ の角 $A$ の二等分線と辺 $BC$ の交点を $D$ とし, 線分 $AD$ またはその延長線上に点 $B$ , $C$ から下ろした垂線の足をそれぞれ $P$ , $Q$ とする. このとき, 点列 $P$ , $D$ , $Q$ , $A$ は調和点列である.

f:id:noriharu-katakura:20210519132739j:plain

$\triangle APB \sim \triangle AQC$ から,

$PA:QA=AB:AC$

$AD$ は $\angle A$ の二等分線だから,

$AB:AC=BD:DC$

$\triangle DPB \sim \triangle DQC$ から,

$BD:DC=PD:DQ$

したがって,

$PA:QA=PD:DQ$

なので, 点列 $P$ , $D$ , $Q$ , $A$ は調和点列である.//

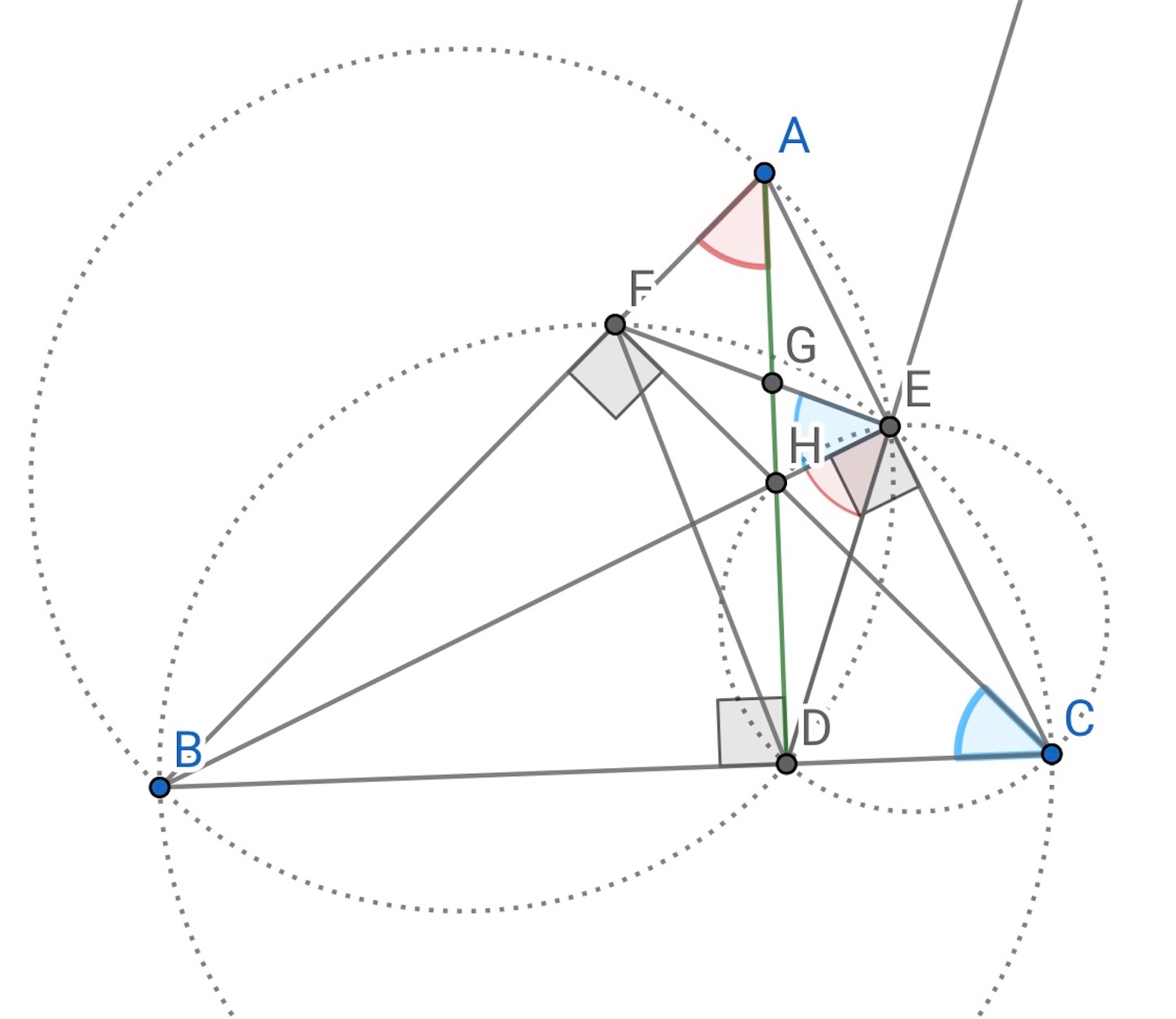
$\triangle ABC$ の垂心 $H$ は, 垂足三角形 $\triangle DEF$ の内心であるから *1, $BE$ は、 $\angle DEF$ の内角の二等分線であり (円に内接する四辺形を追っていけば証明できる), $AE$ と $BE$ は直角なので, $AE$ は $\angle DEF$ の外角の二等分線である. $\triangle EGD$ を考えれば, $DH: HG = ED:EG$ であり, また, $DA: AG = ED:EG$ であるから, $DH: HG = DA:AG$ となり, 点列 $D$ , $H$ , $G$ , $A$ は調和点列である.

f:id:noriharu-katakura:20210604020656j:plain

*1: $\triangle DEF$ からみると $A$ , $B$ , $C$ は傍心である.