陥没地帯 (100) - ノリの悪い日記

塾で高校生に物理を教えている。何をしているかというと、たとえば、慣性の法則がいかに不気味な法則であるかを気長に例をだしながら言い続けているだけである。作用反作用の法則や、遠心力や、内部エネルギーについても同じである。たいした経験もまだしていないが、その不気味さに少しでも気がついた子は物理の成績が大幅に上がったと思う。

うまくできなかったことも沢山あって、「ケプラーの法則」なんかがそうである。なぜ万有引力によって、惑星が楕円軌道 (一般には太陽が焦点の位置にある円錐曲線) を描くのかについて、R. P. ファインマンの素晴らしい幾何学的証明 *1があるのを知っていながらとうとう触れなかった。それで、ここにちょっと書いておく気になった (微分方程式を作り、それを解いて証明するつもりはもともとなかった。なぜかは自分でやってみればわかると思う) 。

ファインマンの証明の方針は、楕円であることがわかっている軌道 (極座標 $r(\theta)$ で表されているとする) とすべての角 $\theta$ で接線の傾きが等しい別の軌道があるならば、スケールはどうであれ、その軌道もやはり楕円軌道だというものである。なお、僕のもっている高校の参考書には、ケプラーの第一法則は、「惑星は太陽をひとつの焦点とする楕円上を運動する」とある。

それでまず、テンプレートとなる楕円軌道と接線を以下のようにして構成している。

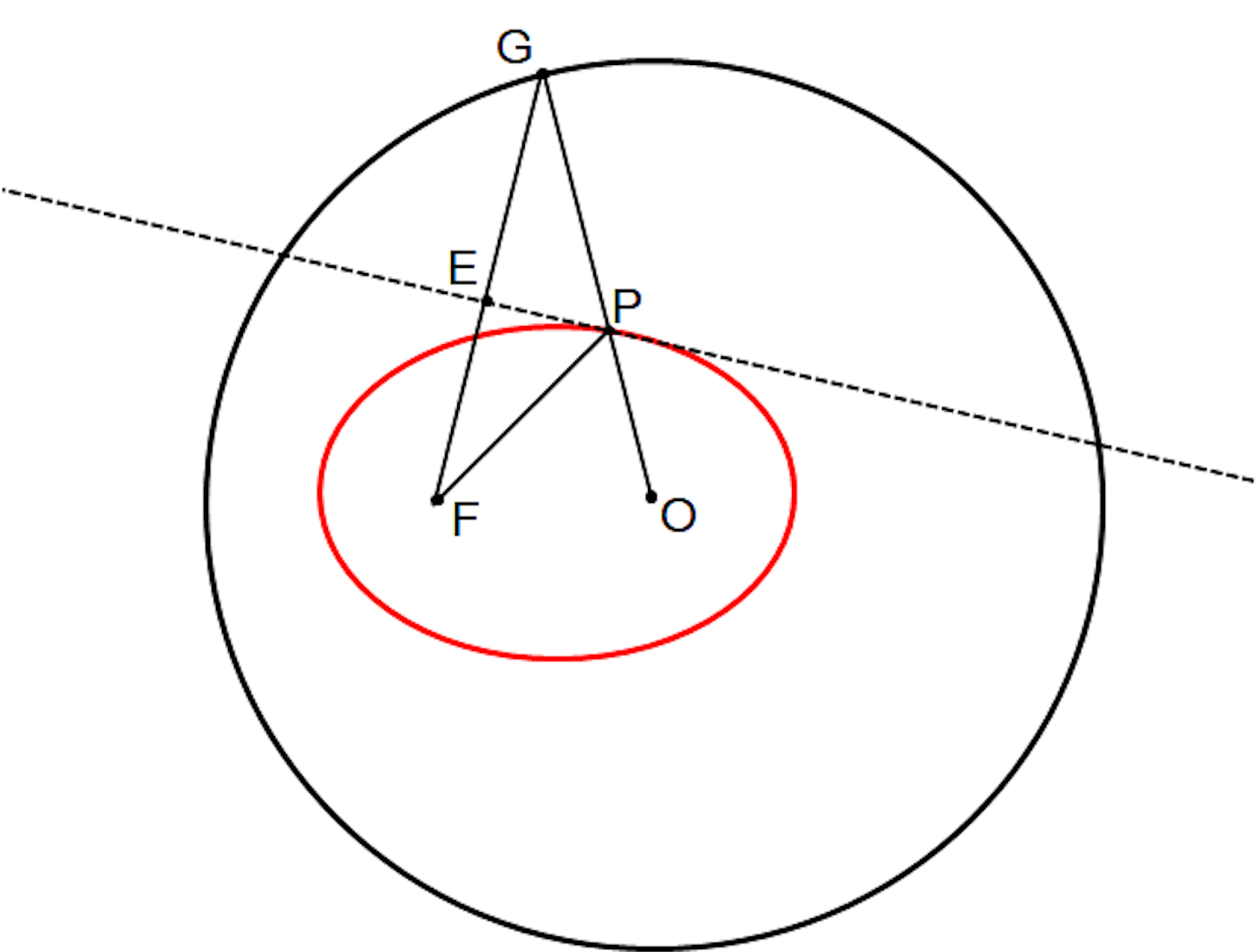
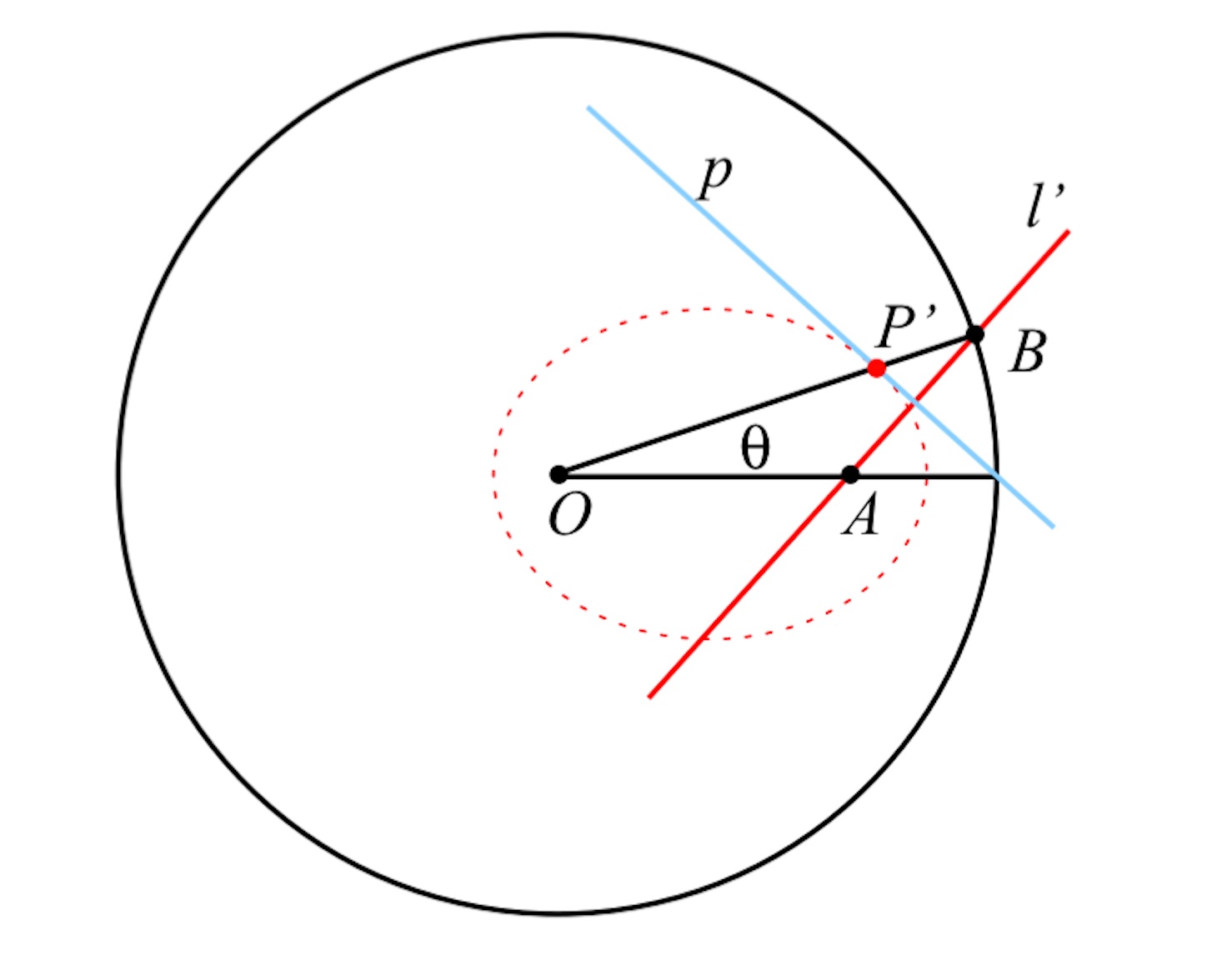
構成の手順はいろいろあるだろうが、たとえば次のようなやり方である。まず、点 $O$ を中心とする円を書く。円の内部に中心 $O$ とは異なる点 $F$ をとる (離心率が 0 より大きく 1 未満の場合に相当)。円周上の点 $G$ を円周上だったらどこでもよいからとり、 $G$ と $F$ 、 $G$ と $O$ を線で結ぶ。線分 $GF$ の垂直二等分線を書き (図の点線)、 $GF$ , $GO$ との交点をそれぞれ、 $E$ 、 $P$ とする。

すると $P$ は楕円上の点であり、点線は接線である。あとは $G$ を動かせば楕円と各点の接線が構成できる。*2

$P$ が $O, \ F$ を焦点とする楕円の周上の点である証明は簡単で、 $OG$ が円の半径で、 $GP=PF$ から、 $OP+PF$ が定値となるからである。点線が点 $P$ における楕円の接線になるのは、点線上にどこでもよいから点 $P$ 以外の点 $X$ をとれば $GX + XO \gt GO$ という三角不等式が成立するので $X$ は楕円の外側の点ということになり、ということは点線は楕円上の一点 $P$ のみを通る接線である。

それで証明すべきことは惑星の運動が楕円軌道を描くということであるが、座標系としては極座標で、太陽を原点にとり、惑星の位置を始線からの角 $\theta$ 、太陽と惑星までの距離 $r$ であらわすことにする (もちろん $r, \ \theta$ は時間 $t$ の関数である)。ファインマンがユニークなのは、軌道を等時間間隔 $\Delta t$ ではなくじゅうぶん小さな等角度間隔 $\Delta \theta$ に分割して考察したことである *3。 $\Delta \theta$ における太陽と惑星の軌道が掃く三角形が作る面積は、 $r^2$ に比例する。 $\Delta \theta$ 移動するのにかかった時間を $\Delta t$ (もはや等時間ではない) とする。ケプラーの第二法則は、角運動量保存の法則 *4と等価である「惑星と太陽を結ぶ線分が単位時間に描く面積は一定である」ということだが、言いかえれば「惑星が軌道を進んだ時間は、惑星と太陽を結ぶ線分が、その時間に掃いた面積に比例する」ということなので、 $\Delta t$ は、 $r^2$ に比例する。一方、万有引力の法則は $r^2$ に逆比例する法則であり *5、 $\Delta \theta$ の間の速度変化を $\Delta v$ とすると、 $\frac{\Delta v}{\Delta t }$ は $\frac {1}{r^2}$ に比例し、 $\Delta t$ は $r^2$ に比例したから、 $\Delta v$ の大きさは一定であるという重要な結果が得られた。距離の自乗に反比例する中心力が働く場合には、軌道が同じ角進む間の速度変化の大きさはいつも同じなのである。

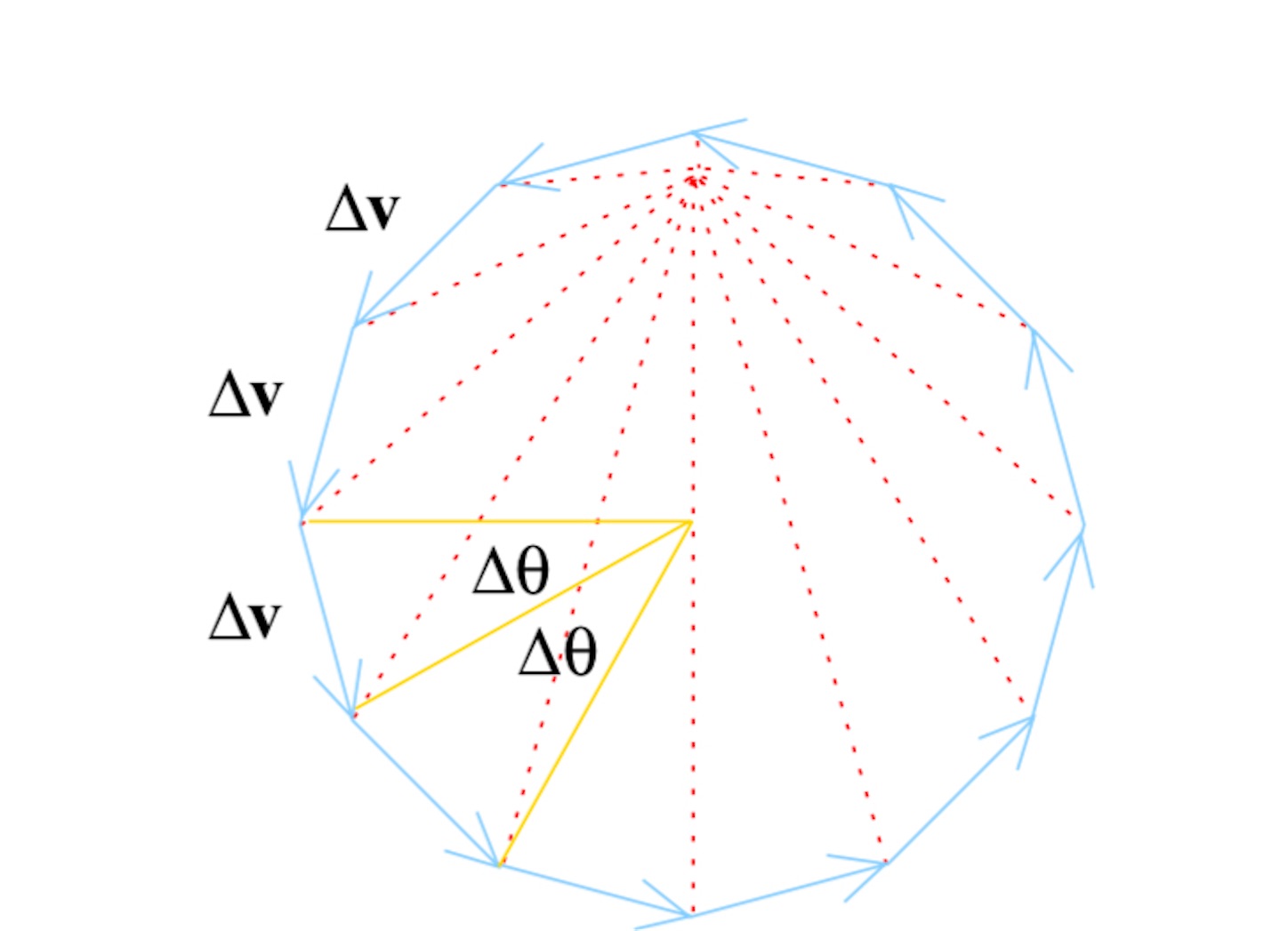
これから少し説明をはしょるが、各 $\Delta \theta$ の速度ベクトルの矢印の始点を共通の点に揃えた速度図 (ホドグラフ) を作ると、 $\Delta v$ が一定であることから下のような図を作ることができ、これは正多角形である。万有引力は中心力であることから、 $\Delta v$ は元の軌道では常に太陽の方を向くので、隣接する $\Delta v$ と $\Delta v$ のなす角は $\Delta \theta$ であり、このことから、正多角形の中心と、一辺のなす角も $\Delta \theta$ であることが容易にわかる。 $\Delta \theta$ を $0$ に近づけていくと、正多角形は円に収束していくと考えることができる。つまり、距離の自乗に反比例する中心力が働く場合には、速度図は常に円を描く。

あとは、惑星の角 $\theta$ の速度ベクトル (速度ベクトルの方向はその位置における接線 $l$ の傾きである) に対して、

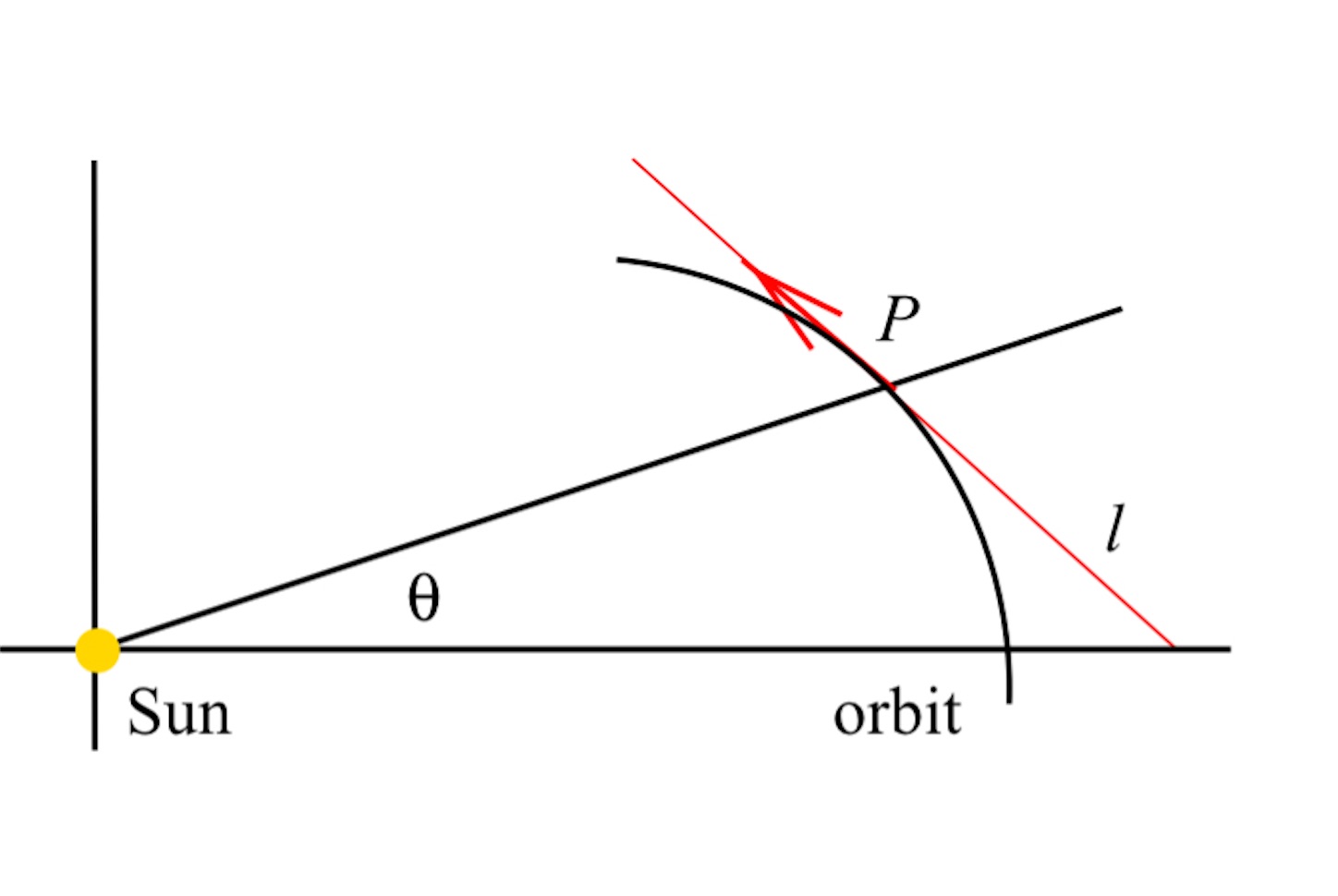
対応する速度図に速度ベクトルが平行になるように移す。このとき、 $OA$ と $OB$ のなす角が軌道と同じ $\theta$ になることが重要である。

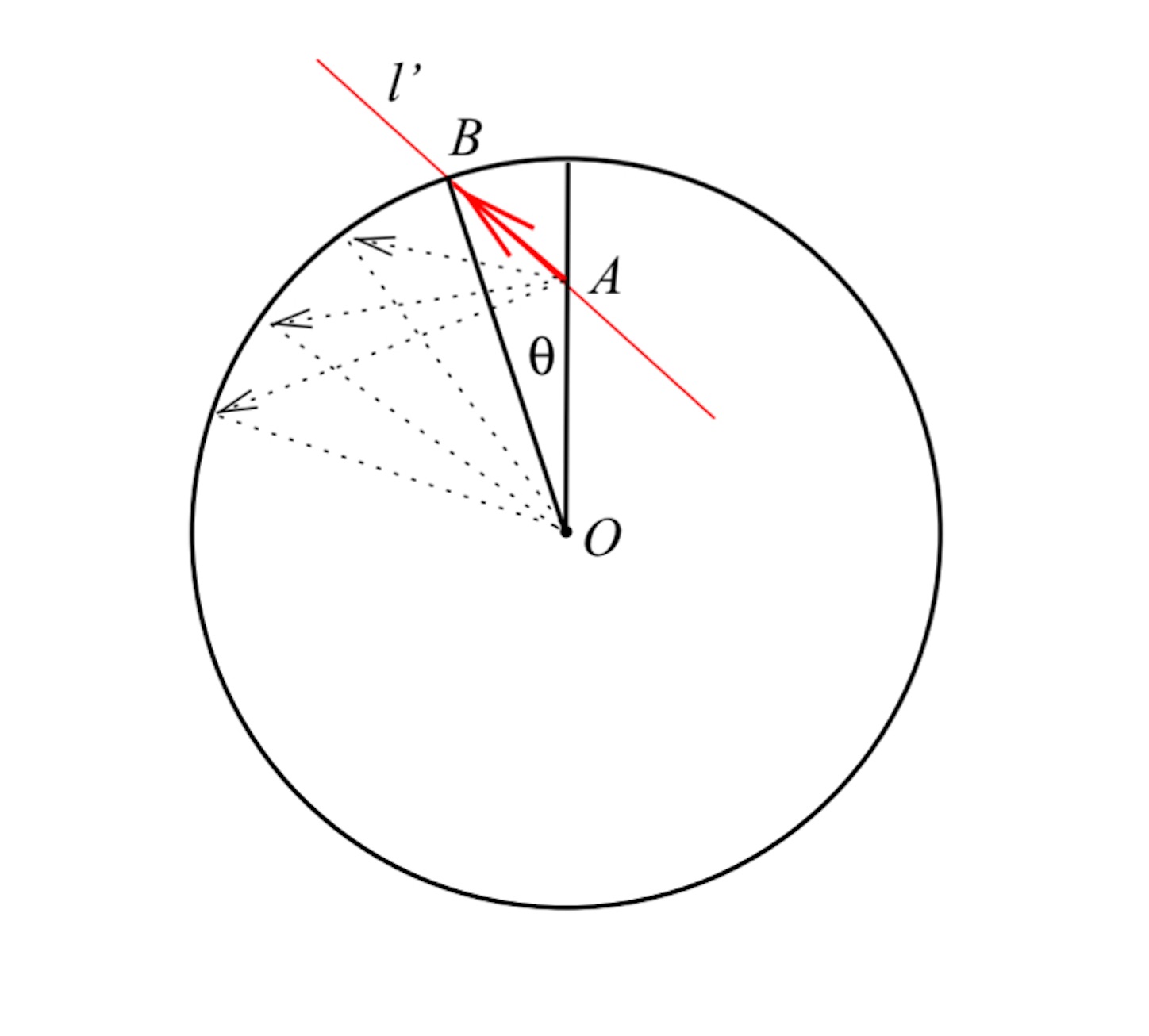
これもなかなか気付きにくいが、この図を $90$ 度 (時計まわりに) 回転させてから、最初にやったやり方で $O$ と $A$ を焦点とする楕円を構成する。 $l'$ は前の図から $90$ 度回転しているので、接線 $p$ は軌道の接線 $l$ と平行である。この関係は任意の $\theta$ で成り立つのだから、一番最初の証明の方針が実現できており、もとの軌道も楕円であると結論できる。

参考までに、ここでは計算しないが、惑星の角運動量の大きさを $L$ 、万有引力定数を $G$ 、太陽と惑星の質量をそれぞれ $M, \ m$ とすれば、速度図の円の半径は、 $\frac{GMm}{L}$ と求めることができる。

※ R.W.Hall, N.Higson の “Paths of the Planets” (1998) から、図を引用させていただきました。

*1:David L. Goodstein and Judith R. Goodstein. Feynman’s Lost Lecture : the motion of planets around the sun. W. W. Norton & Company, New York, 1996. 邦訳は『ファインマンの特別講義』岩波現代文庫。かつて出版されていた『ファインマンさん、力学を語る』が改題されたもの。

*2:補足として、点 $F$ を円の外側にとると (離心率が 1 より大きい場合に相当)、同じやり方で双曲線とその接線が構成できる。双曲線の場合は下の証明で　 $|OP-PF|$ が定値 (円の半径) になることを確認すればよい。なお、双曲線は 2 種類構成できるが、実際に実現できるのは力学的エネルギー保存の法則を満たすもののみである。点 $F$ を円周上にとったとき (離心率が 1 に相当)、放物線とその接線はこのやり方では構成できない。放物線の構成方法は、以下を参照してほしい。なお、放物線に相当する軌道を描くのは、高校物理でも学習する第二宇宙速度の場合である。Michael Kowen, H. Mathur. On Feynman's analysis of the geometry of Keplerian orbits Am. J. Phys., Vol. 71, No. 4, April 2003 [PDF] On Feynman’s analysis of the geometry of Keplerian orbits | Semantic Scholar

*3:分割に伴い万有引力も撃力近似される

*4:力の作用線が回転中心を通る中心力では万有引力に限らず一般に成立する。

*5:ケプラーの第三法則は、「(太陽のまわりを回る) すべての惑星の公転周期 $T$ の $2$ 乗は、楕円軌道の長半径 $a$ の $3$ 乗に比例する」というものだが、これを楕円の特別な場合である円運動にあてはめてみる。向心加速度は $\frac{v^2}{a} =(\frac{2\pi }{T})^2a$ であり、 $T^2$ は $a^3$ に比例するのだから万有引力は、距離の $2$ 乗に逆比例する。なお、円運動の向心加速度の大きさは、後に出てくる速度図で考えれば、 $\frac{2\pi v}{T} = \omega v$ に等しいことから容易に求められる。